授業の基本情報
授業名 : ベクトル解析
開講部局 : 教養学部(前期課程)
対象 : 学部 2 年生(選択)、工学部の学生も 1 割程度参加
学生数 : 約 200 名
形態 : 全てリアルタイム
利用したツール :
- ITC-LMS: 学習管理システム(課題の配布、学生へのフィードバック)
- Zoom: オンライン会議システム、(リアルタイム授業、チャットでの質問)
- Tex: 組版処理システム(講義資料の作成)
- Adobe Illustrator: ベクターイメージ編集ソフトウェア(講義資料の図の作成)
- Mathematica: 数式処理システム(講義資料の図の作成)
教員の基本情報

加藤 晃史 先生
数理科学研究科
准教授
学生のコメント: この授業が良かった理由
学生 A のコメント
300 ページを超える資料を作っていただいて予習復習が捗った。
学生 B のコメント
配布資料が充実していた。録画などが公開されていて復習がしやすい。成績評価のための小テストやレポートがスムーズでトラブルがなかった。
学生 C のコメント
事前に詳細な講義ノートが作成・配布されたことと、講義の録画が講義終了後速やかに全員に提供されたため、極めて効率よく学習を行うことができた。
従来は講義資料なし、教科書指定なしの講義が多く、予習できないまま教室に行き、初めて聞く話を教員の好きなペースで展開されてしまい、説明の音声は直ちに消えていくという著しく非効率な状況であったが、今学期は幸いなことに教室での対面講義が封じられたことで、講義資料の事前配布や録画の事後提供が行われる講義が増え、学習の効率性が飛躍的に高まった。
授業をオンライン化するにあたって心がけたこと
これまで、授業は板書を使って進めていたのですが、今回は自作の配布資料を用意しました。リアルタイムで板書を書いても、回線の問題でうまくその動画が送れないかもしれないという懸念があったからです。そもそも板書は、学生の反応を見ながらそれに合わせて授業が進められるというところにメリットがあるのであって、学生の様子が分からないオンライン授業の場合は、前もって作成した資料を配る方がやりやすいだろうと判断しました。配布資料にしたおかげで、学生が予習復習をしやすくなるなど、オンライン授業ならではの良さが提供できたのではないかと思います。
期末試験については、うまく行われていた先生もおられますが、私はオンラインで公平性を保ったまま実施することは難しいだろうと思いました。そこで、いつもは 1 回の最終テストで成績を付けていたのですが、今回は最終回を除く各授業で課題を提示し、その提出状況や出来によって成績評価を行うことにしました。試験では他人の答えを見てはいけませんが、今回の課題は各自で調べたり他人に聞いたりするのは自由とし、使えるものはなんでも使ってもらいました。私の方から、参考になりそうなサイトの共有なども行っています。また、学生の方からも、様々なサイトやアプリケーションを教えてもらいました。今回は課題で成績評価を行うことにしたため、これまでの期末試験のような生徒の理解度を測るための課題ではなく、理解度を上げるための課題にするようにも心がけました。
工夫したところ
詳細な図入りの配布資料を作成した
配布資料の長さは 300 ページ近くにもなりました。教科書にしたいくらいのボリュームですね。更新を繰り返し、最終的に配布したのは「version6.1」です。ただ、なかなかの自転車操業で、学生が誤植を指摘してくれることもありました。特にこだわったのは「図」で、Mathematica や Adobe Illustrator を使って学生の理解を助けることのできるようなものを多く挿入しました。
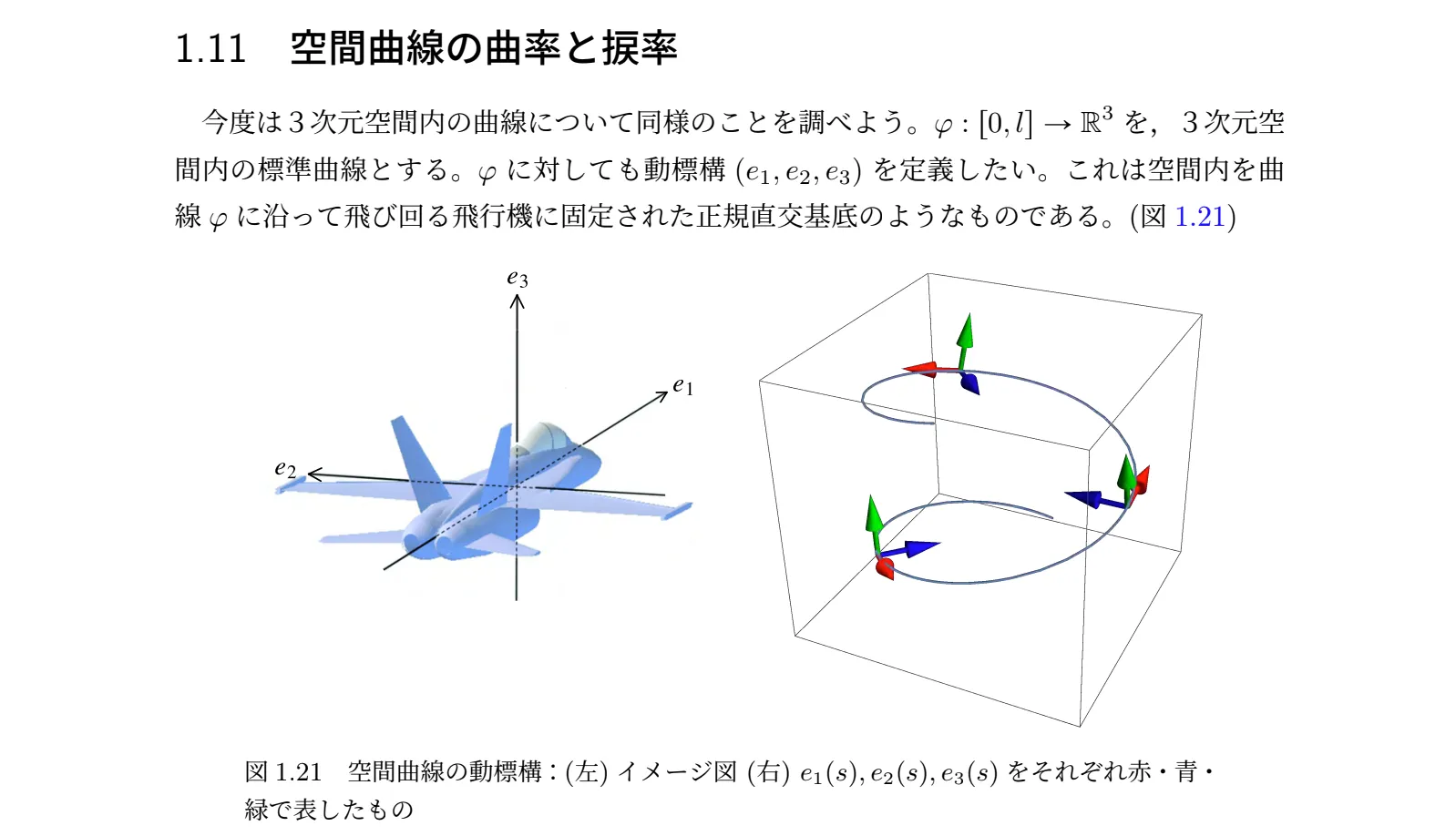
図を多く入れたのは、個人的な趣味もありますが、やはり「百聞は一見にしかず」だと思っているからです。
授業では、配布資料と同じことを話しても仕方ないので、より学生に内容を理解してもらえるよう、身近な例に喩えて数学の概念を説明するといったことを重点的に行っていました。
毎週提出の課題による成績評価を実施し、そのフィードバックを行った
試験による公平な評価は難しいと感じたため、毎週提出する課題によって成績評価を行いました。最終回を除く、計 10 回の提出です。毎週提出の課題にしたからには、試験のように学生の理解度を測るのではなく、学生の理解度を高めるようなものにしたいと思いました。ですから、学生が提出した全ての課題に対して、何かしらのフィードバックを行っています。フィードバックには ITC-LMS を用いました。ただ、これは学生と往復のやりとりを行うにはあまり適していなかったので、改善に期待したいですね。約 200 人にも及ぶ学生の提出物に毎週コメントしていくのは骨が折れる作業で、後半は十分な回答ができなかったこともありましたが、できる限りやりました。従来は期末試験のみだったので、学生の顔色以外の反応が得られなかったのですが、今回は毎週の課題提出とフィードバックがあったので、学生と交流しながら授業を進めていくことができました。そういった意味でも、毎週課題を提出する方式にして良かったと感じています。
提出してもらう課題の内容自体も、ただの問題ではなく、自由研究的な要素を持つ、やっていて楽しい課題を出すように心がけました。例えば、「各自で曲線をデザインする」という課題では、ハート型やト音記号など、変わった形のグラフを描く数式を導いてもらいました。専用のソフトを用いて、各々が自由に数式を考えてくれましたね。次の授業の課題は、自分が作ったグラフの線分の長さを測ってもらうというものでした。数値計算のソフトを使って取り組んでもらいました。これも、オンラインならではの取り組みだったのではないかと思います。
苦労したところ
配布資料の作成が大変だった
やはり配布資料を作成するのには苦労しました。図まで挿入しているので、作るのに時間がかかります。今学期に私が受け持っていたのはこの「ベクトル解析」の授業だけだったのですが、もし他にも授業を担当していたとしたら、ここまでの配布資料を作成することはできなかったと思います。
ITC-LMS が使いにくかった
フィードバックを毎週行うのも大変だったのですが、ITC-LMS で学生とやりとりする環境がもう少し整っていれば、少し楽になっていたかもしれません。ITC-LMS 上の情報を検索するのに、10 ステップ近くかかってしまうということにも苦労しました。しかし、特に問題だったのは、提出物の取り違えがあったことです。ITC-LMS のシステム上のトラブルで、提出した課題が学生の間で入れ替わってしまっていたのです。学生とフィードバックでやりとりをしている過程で指摘されたのですが、もし指摘されていなければそのまま評価を付けてしまっていたかもしれません。Google Classroom も使いやすいという話を聞いたのですが、UTAS と連携してない点が不便なので、やはり今後も ITC-LMS を使っていくかと思います。ただ、実際に授業をやっていく上で感じた改善点は、個人的に ITC-LMS の担当者の方に伝えているので、今後直っていくかもしれません。
今後のオンライン授業に向けて
A セメスターでは専門の授業になるため、教養の授業を受け持っていた S セメスターとは勝手が違います。今回は配布資料を用いましたが、次は板書でやろうかと思っています。専門の話だと図が描きにくくなってきますし、やはり資料を作るのはなかなか大変なので。それと、教養の授業と比べて人数が大きく減るので、個別にフィードバックがしやすくなるからという理由もあります。
ただ、教養の授業で配布資料を用いたのは良かったと思います。専門の授業とは違い、教養の授業は、この授業以降に人生で数学を勉強することがないような人も受けています。この東大で数学嫌いを作ってしまっては、日本の理系の未来がなくなってしまうという思いがあるので、できるだけ良いイメージを持ってほしいのですが、配布資料はそれに役立ったと思います。配布資料は使い回すことができると思うので、今後はフィードバックに時間が取れるのではないかと期待しています。
参考情報
本授業の概要(シラバスより)
1 年生で学んだ「微分積分学」において実数を値に持つ関数の微積分を扱ったが, 自然科学では運動する点の速度のようにベクトルに値を持つ時間の関数や, 各点の電荷密度のように空間上の関数などが, よくあらわれる. さらに電磁気学における磁場のように, 空間上の関数であってベクトルに値を持つものが扱われることも多い, ベクトルに値をもつ関数はベクトル場と呼ばれ, 実数に値をもつ通常の関数はスカラー場とも呼ばれる. そのような種々の関数があらわれ, 微積分学的な性質とベクトルのもつ性質が組み合わさって重要な役割を演じる自然現象が, 電磁気学や流体力学をはじめとして数多くの場面で見かけられる. 本科目では自然現象の記述と考察に適用できるそのような数学的枠組みについて解説する.
授業内容
講義内容はおおむね以下の通りであるが,担当教員によっては順序や内容に一部変更が加えられる場合がある.
1.曲線,曲面上の積分
パラメータ表示された曲線上のベクトル場の線積分や,パラメータ表示された曲面上の関数やベクトル場の面積分の定義をする.また,曲線および曲面の接ベクトルや法ベクトルなどの幾何学的概念について考察し,曲線の長さ,曲面の面積などの定義とその計算法について学ぶ.
2.関数,ベクトル場とその勾配,発散,回転
関数に対する勾配,またベクトル場に対する発散および回転の定義とその幾何学的意味について解説する.
3.微積分学の基本定理の拡張:勾配と線積分
関数の勾配によりあらわされたベクトル場の線積分と,その関数との関係を考察する.
4.グリーンの定理とガウスの発散定理:発散と領域上の積分
平面領域における2重積分と,その境界における線積分との関係である,平面におけるグリーンの定理について学ぶ.さらに,空間領域における3重積分と,その境界における面積分との関係である,ガウスの発散定理および空間におけるグリーンの定理について学ぶ.ここではベクトル場の発散が用いられる.
5.ストークスの定理:回転と面積分
3次元空間内の曲面における面積分と,その境界における線積分との関係である,ストークスの定理について学ぶ.ここではベクトル場の回転が用いられる.
6.微分形式
勾配と線積分の関係,グリーンの定理,ガウスの発散定理,ストークスの定理を系統的に記述するための記法としての微分形式とその外微分について解説する.さらに線積分,面積分,3重積分を微分形式の積分として統一的に定式化する.
具体的な授業 1 回分の流れと方法
教員が参考資料を共有しながら、それを元に説明していきます。授業の最後の 10 分間は質疑応答の時間とし、学生がチャットで行った質問に答えました。質疑応答は授業中でも可能です。
評価方法
毎週提出の課題で評価しました。
課題の提出は、最終授業を除いた計 10 回で、その合計で評価しました。昨年度までは、期末テストで成績評価を行っていました。
分量は、毎回 A4 用紙 2 枚に収まる程度であり、やや多いですが、授業を履修者の多くが時間に余裕のある 2 年生だということを踏まえたものになっています。
曲線をデザインする数式を導出するものや、自分で導き出した曲線の線分の長さを測るものなど、自由研究形式で楽しんで取り組める課題です。提出期限は課題提示から 2 週間後であり、その期間以内に提出すれば、サイトなどは自由に使って良いことになっています。参考にすべきサイトが、教員から提示されることも多いです。